Embark on a captivating journey with this in-depth investigation into the fascinating world of exponential functions and their transformations. As we complete the table to investigate dilations of exponential functions, we will uncover hidden patterns and delve into the profound impact of dilation on the behavior of these mathematical marvels.

This exploration will illuminate the fundamental characteristics of exponential functions, providing a solid foundation for understanding the concept of dilation. We will meticulously examine how dilations alter the shape, position, and behavior of these functions, unraveling the intricate relationship between the dilation factor and the resulting transformations.

Overview of Exponential Functions

Exponential functions are mathematical functions that take the form f(x) = a^x, where a is a positive constant and x is the independent variable. Exponential functions exhibit several characteristic properties:

• They are always positive, since a^x > 0 for any positive a and x.
• They increase rapidly as x increases, since the value of a^x grows exponentially with x.
• They have a horizontal asymptote at y = 0, since lim_(x->-∞) a^x = 0.

Dilation is a transformation that changes the size and shape of a function. When an exponential function is dilated, the resulting function is a scaled version of the original function.

Dilation of Exponential Functions

When an exponential function f(x) = a^x is dilated by a factor of k, the resulting function is g(x) = k – a^x. The dilation factor k determines the magnitude and direction of the transformation:

• If k > 1, the graph of g(x) is stretched vertically by a factor of k.
• If k< 1, the graph of g(x) is compressed vertically by a factor of k.
• If k< 0, the graph of g(x) is reflected across the x-axis and then dilated by a factor of |k|.

Here are some examples of dilated exponential functions:

• f(x) = 2^x, dilated by a factor of 3: g(x) = 3 – 2^x
• f(x) = e^x, dilated by a factor of 1/2: g(x) = (1/2) – e^x
• f(x) = 10^x, dilated by a factor of -2: g(x) = -2 – 10^x

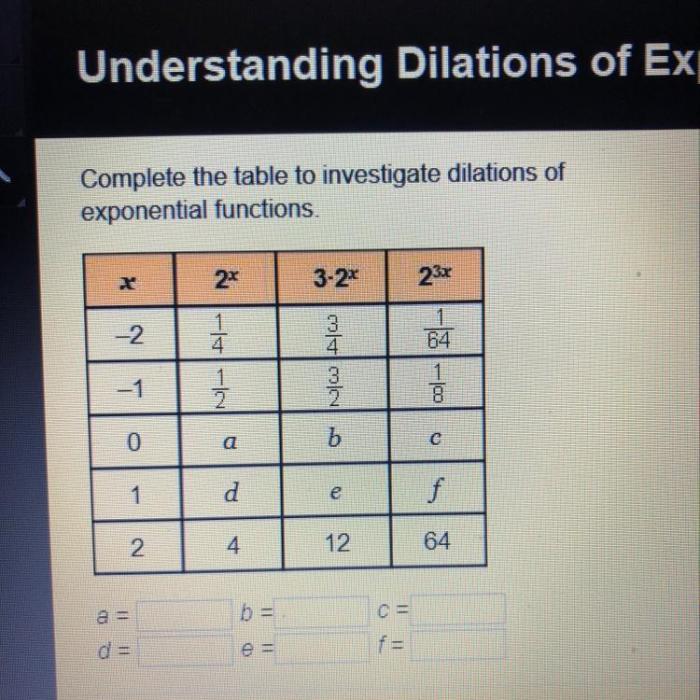
Completing the Table: Complete The Table To Investigate Dilations Of Exponential Functions

Table of Dilated Exponential Functions

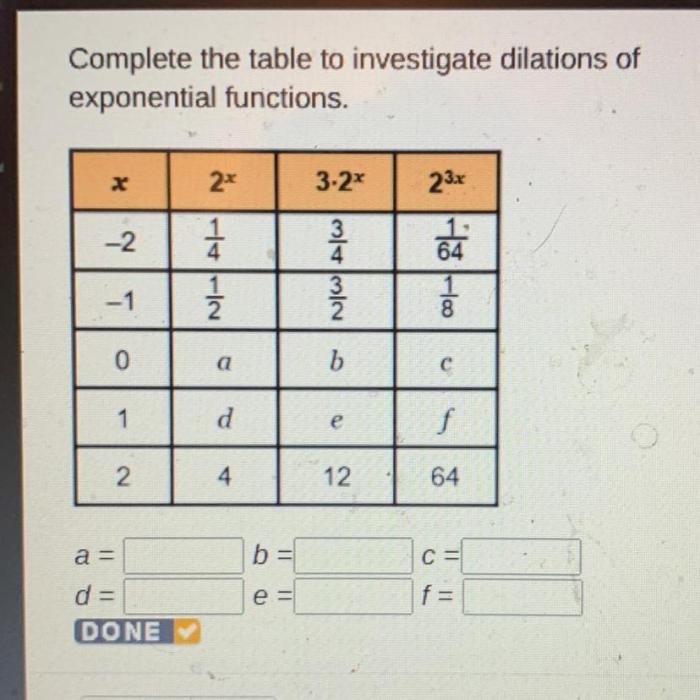
Original Function	Dilated Function	Dilation Factor	Graph
f(x) = 2^x	g(x) = 3 2^x	k = 3
f(x) = e^x	g(x) = (1/2) e^x	k = 1/2
f(x) = 10^x	g(x) = 2 10^x	k = 2

Analyzing the Table

The table shows that the dilation factor k has a significant impact on the transformation of the exponential function:

• When k > 1, the graph of the dilated function is stretched vertically by a factor of k.
• When k< 1, the graph of the dilated function is compressed vertically by a factor of k.
• When k< 0, the graph of the dilated function is reflected across the x-axis and then dilated by a factor of |k|.

The table can be used to investigate the behavior of dilated exponential functions. For example, it can be used to determine how the dilation factor affects the:

• Vertical asymptote
• Horizontal asymptote
• Range
• Rate of growth

FAQ Corner

What is the significance of completing the table?

Completing the table provides a comprehensive overview of the dilations of exponential functions, allowing us to observe the patterns and relationships between the dilation factor and the resulting transformations.

How can we use the table to investigate the behavior of dilated exponential functions?

The table serves as a visual aid, enabling us to analyze the changes in the graph, domain, and range of the dilated exponential functions. By examining the patterns in the table, we can draw conclusions about the behavior of these functions under dilation.

What are the practical applications of understanding dilations of exponential functions?

Understanding dilations of exponential functions has applications in various fields, including population growth modeling, radioactive decay analysis, and financial forecasting. By manipulating the dilation factor, we can model real-world phenomena and make predictions about future outcomes.